Numération binaire : base 2
Chargement page et sommaire en cours...
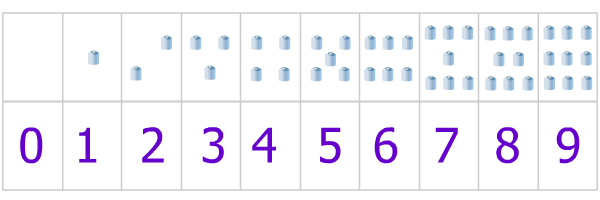
Numération Binaire : rappel sur le décimal
La Base
La base est le nombre de valeurs que peut prendre un caractère nommé chiffre en décimal et bit en binaire.En décimal la base est de 10, on dispose donc de 10 chiffres de 0 à 9 inclus :
En binaire on n'a plus que 2 valeurs : 0 ou 1
Nombre constitué de chiffre(s)Le chiffre est unique, une série de chiffres se nomme un nombre...
En réalité, notre cerveau compte le nombre de chiffres (4 ici) pour affecter la bonne grandeur ou poidsSuivant qu'un chiffre soit seul ou premier d'une liste de 4 comme ici, son importance sera liée à sa positionPositionnez-vous sur chaque chiffre pour en voir le poids ou grandeur au 1° d'entre eux (8 ici), grandeur qui est en l’occurrence le(s) millier(s).
88 ici 8 n'exprime pas que vous possédez 8 oranges ou citrons.
Mais au moins 8 milliers de ces agrumes ! 55 exprime le nombre de centaines 33 est le nombre de dizaines possédées 9Et enfin 9 le nombre d'unités !
N'oubliez pas que la numération en vigueur a été inventé par les arabesChiffres indo-arabes, en mnémotechnique j'utilise cela pour dire qu'on devrait lire un nombre comme les arabes : de droite à gauche, ainsi on commence par les unités, puis dizaines, centaines... Inutile alors de compter le nombre de chiffres (au risque de se tromper)... et qu'il est ainsi judicieux de commencer dans l'autre sens !Mais au moins 8 milliers de ces agrumes ! 55 exprime le nombre de centaines 33 est le nombre de dizaines possédées 9Et enfin 9 le nombre d'unités !
- 8 Milliers
- 5 Centaines
- 3 Dizaines
- 9 Unités
Dépasser 2 valeurs !
Pour exprimer une valeur > à 9 en décimal, on remet le chiffre des unités à 0 et ajoute un chiffre à 1 devant : la dizaine !(quand il est à 0 on ne le représente pas comme en décimal) !
On va voir tout cela et, comme l'illustre l'animation ci-dessous, les conversions !
Méthodes des poids
Système décimal | Système binaire
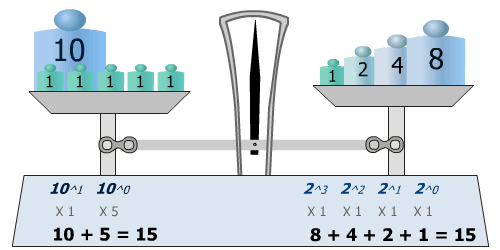
| 1 poids de 10 = 10 5 poids de 1 = 5 Total = 15 10 + 5 = 15 | 1 poids de 8 = 8 1 poids de 4 = 4 1 poids de 2 = 2 1 poids de 1 = 1 8 + 4 +2 + 1 = 15 Total = 15 |
On découvre ainsi que l'on doit utiliser des quantités de poids de chaque base différents en décimal qu'en binaireEn décimal on utilise :
5 × unités
1 × dizaine
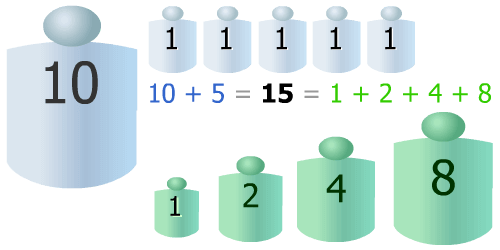
En binaire on utilise :
1 × poids '1'
1 × poids '2'
1 × poids '4'
1 × poids '8'
(Le poids '1' est équivalent au poids unité) !
Animation : comptage décimal
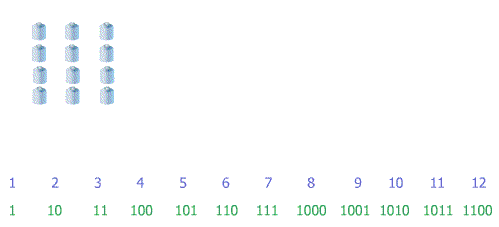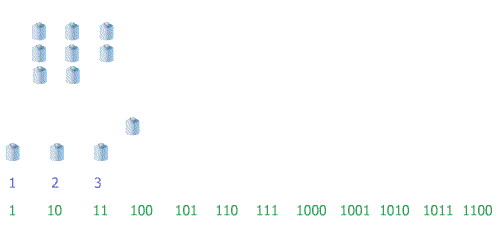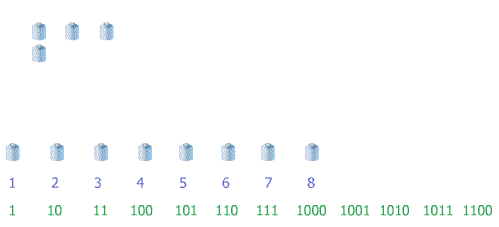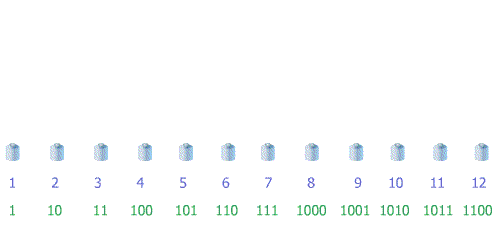
En décimal, on revoit ici que le poids supérieur (appelé plus fort) à gauche s'incrémente quand le poids inférieur (appelé plus faible) à droite dépasse 9 (la fin de sa base) pour revenir à 0.
Il en ira exactement de même en binaire, simplement la dernière valeur ne sera pas ici :
Décimal : 9 (0 à 9 inclus = 10 valeur : base 10)
Mais binaireEn effet, en binaire on est limité à 0 ou 1... : 1 (0 ou 1 = 2 valeurs base 2) !
Base 10 décimal : 10 valeurs
Base 2 binaire : 2 valeurs
Base 2 binaire : 2 valeurs
Un peu de maths : les puissancesLa page suivante avec les conversions, nosu démontrera l'utilité des puissance :
10^0 = 1, 10^1 = 10, 10^2 = 100...
2^0 =1; 2^1 = 2, 2^2 = 4...
Animation : comptage en binaire
L'animation ci-dessous nous montre l'équivalence :
Binaire en bleu versus Décimal en vert
Invité, affichez le quiz :
0
Cours extrait du stage : INDUSTRONIC
Stage : INDUSTRONIC
