La table de vérité !

Pourquoi une table de vérité ?

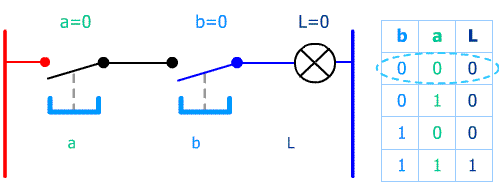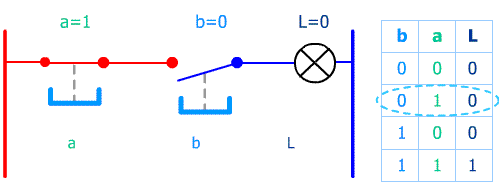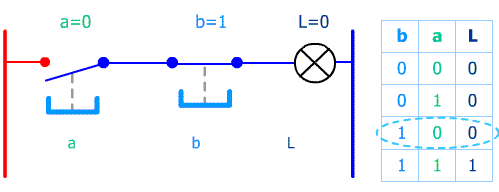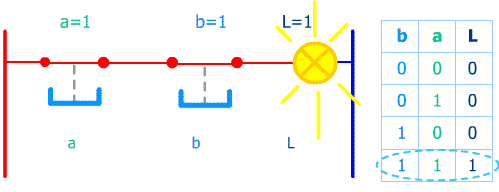
Avec un exemple très simple : 2 poussoirs (entrées) et une lampe (sortie) nous allons comprendre l'intérêt d'une table de vérité :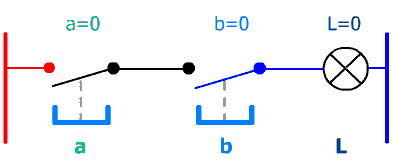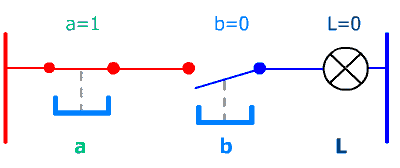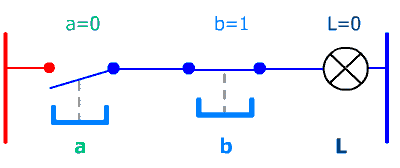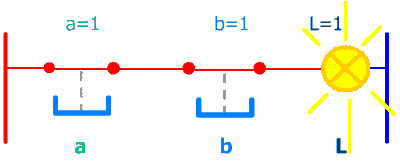

Après un moment d'observation il apparaît ici clairement que la lampe s'allume quand les 2 poussoirs sont simultannément pressés.
En language d'automaticien : Sortie L = entrée a ET entrée b
Un outil peut nous aider à ne rien oublier : la table de vérité qui va nous dire : toute la vérité, rien que la vérité...

Représentation d'une table de vérité

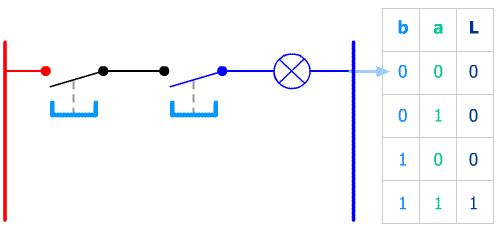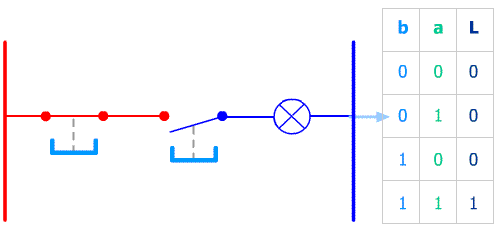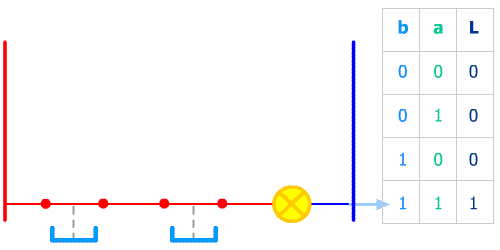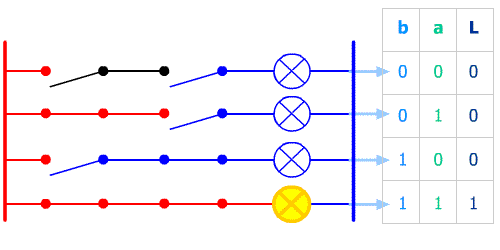
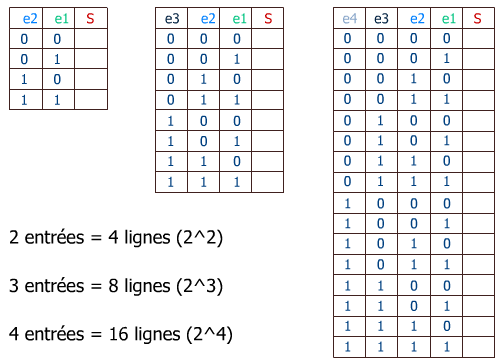
Puisque chaque entrée, qui conditionne la sortie, ne peut prendre que 2 états, il suffit d'écrire les 2 états de chaque entrée en s'inspirant du comptage binaire :
Une entrée au poids 0 chaque à chaque ligne, la seconde ne change que lorsque la suivante aura pris ces 2 états.
On peut constater que le nombre de lignes doubleraLe nombre de lignes est égal à la valeur décimale de la base exposant le nombre de conditions d'entrée :
2 entrées = 4 lignes 2^2 ; 3 entrées = 8 lignes 2^3 ; 4 entrées = 16 lignes 2^4...

La table de vérité est à réserver à des systèmes présentant un nombre d'entrées contenu ! pour chaque condition d'entrée supplémentaire.
Une table de vérité peut comporter plusieurs sortiesSi une seconde lampe par exemple ne s'allume elle que lorsque le poussoir 'a' est sollicité :

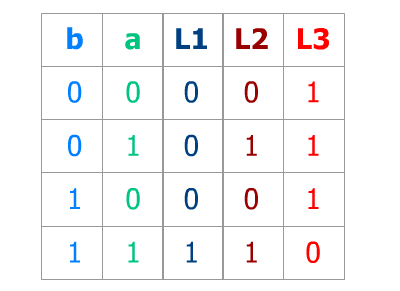
Par contre, il aurait été plus judicieux ici de simplifier : L2 n'est conditionné que par 'a', une seule entrée ! Pour L3 en revanche, elle est l'opposée de L1... L3 = L1/, on va voir tout cela !...

Animation sur table de vérité

L'avantage de cette table réside dans l'écriture de toutes les possibilités ce qui permet une analyse complète.
Son inconvénient est justement lié à cet avantage : la table peut rapidement devenir illisible dès que l'on dépasse 4 entrées !