Déphasage cosinus φ facteur de puissance
Chargement page et sommaire en cours...
Le triangle des impédances
Objectif de la représentation
Les grandeurs à ajouter n'étant pas en phase, il convient d'effectuer une somme vectorielleEn effet, comment ajouter, des intensités en l'occurrence, qui sont quasiment opposées à 180° ?Cela revient à ajouter un bénéfice et une perte sans le signe – :
J'ai gagné 50 € et j'ai perdu 30 €, j'ai donc 80 €...
Non, il faut effectuer 50 – 30...
Mais dans notre cas, c'est encore plus complexe puisque la bobine est imparfaite et ne déphase que de 72°, on ne peut donc pas effectuer de soustraction....
En représentant les intensité comme des vecteurs, on va tenir compte de leur déphasage réel et il suffira d'appliquer Pythagore pour effectuer des opérations...
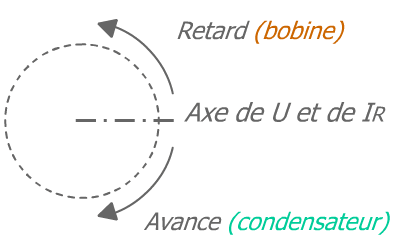
Grâce au cercle trigonométrique on pourra comprendre le bloc suivant sur le redressement du cosinus phi (cosφ).
Le temps s'écoulant dans le sens trigonométrique le retard de la bobine est représenté en sens anti-horaire, le condensateur en 'avance' : dans le sens horaire.
Le cas de la bobine, déphasage < 90°
Pourquoi le déphasage d'un composant parfait (le condensateur en est extrêmement proche) doit être de 90° ?Tous les 90°, soit 1/4 de période, le signal s'inverse : il change de sens ou de polarité !
C'est donc à ce moment que l'intensité dans les récepteurs capacitifs ou inductifs parfaitsInductance pure L en Henry d'une bobine théorique puisque débarrassée de toute résistance due au fil la constituant. elle aussi s'inverse, ou change de polarité : par réaction.
On nomme X cette impédance imaginaire théorique : X = réactance : son petit nom.
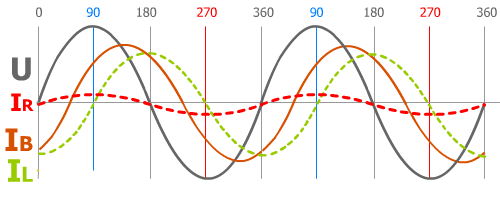 | |
| En vert l'inductance pure L (qui se mesure en Henry) de la bobine avec le signal IL théorique, imaginaire, déphasé de 90°. En marron le déphasage réel IB dû à l'impédance Z de B la bobine qui combine (dessin de droite) l'impédance X de L (son inductance) et en rouge sa résistance R = (ρ × lg) / S ; R dont l'intensité IR (en rouge) est en phase avec U. IB↗ = IR↗ + IL↗ | 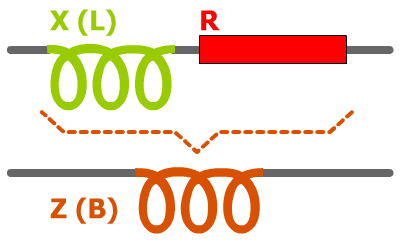 |
Triangle des impédances : la bobine
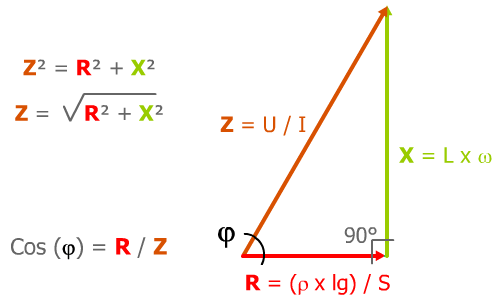
R est dans l'axe puisque non déphasé.
X est vertical, à 90°, il représente L l'inductance parfaite

L en vert, B étant la résultante de L et R de notre bobine.
Z la résultante, la bobine réelle forme un angle que l'on peut obtenir de 2 manières :
- En mesurant l'angle à l'oscilloscope
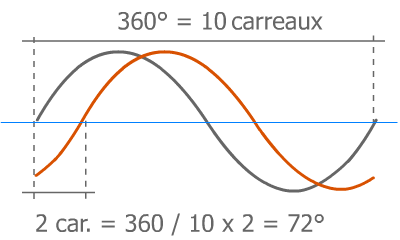 et appliquant une simple règle de 3
et appliquant une simple règle de 3 - En utilisant Pythagore puisque l'on connait 2 grandeurs R et Z, il suffit d'appliquer les règles sur les angles (cosinus,...) vu dans les conseils+ fin de page
La méthode 1 avec l'oscilloscope en image

Méthode 2 : Pythagore nous permet de connaître, au besoin, le coté manquant : X bobine = √(Z² - R²)
Quant à l'angle de déphasage on prendra les valeurs de notre exemple (en vidéo un peu plus haut) :
R = 15 Ω ; Z = 90 Ω
Connaissant donc l'hypoténuse Z et le coté adjacent R de l'angle φ (phi) recherché on utilisera le plus approprié : Cosinus = coté adjacent / hypoténuse (voir conseils+)
Donc dans notre cas :
Cosφ = R / Z ; Cos φ = 15 Ω / 90 Ω = 0.167
Pour trouver l'angle, calculatrice recommandée avec fonction Cosécante (INV. Cosinus)Cosécante, cosec, csc, arcos, Cos-1, Inverse Cos... tout dépend de votre calculatrice :
INV. Cos (0.167) = 80°, pour 72° lus graphiquement à l'oscilloscope.
L'incertitude est de 10% environ, ne vous en formalisez pas, la précision n'était pas l'objectif premier !
'Triangle' du condensateur :
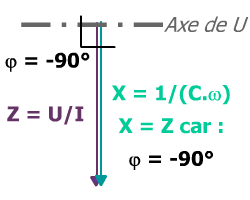
Pour le condensateur c'est plus simple !
Le déphasage étant de 90° exactement, l'angle entre Z et R est de 90°, cos(90°) = 0 !
Tout comme cosφ = R / Z
cosφ = 0 / Z = 0 !
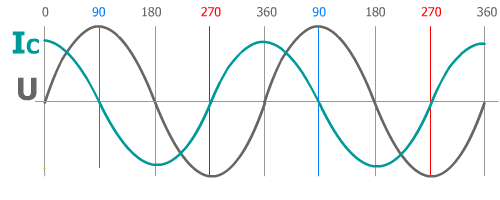 Le condensateur voit son impédance imaginaire (théorique parfaite) X confondue avec son Z car, considéré parfait, il engendre exactement 90° de déphasage.
Le condensateur voit son impédance imaginaire (théorique parfaite) X confondue avec son Z car, considéré parfait, il engendre exactement 90° de déphasage.Ce qui est intéressant à retenir est la quasi-opposition entre IB et IC permettant de deviner que leur somme donnera une valeur inférieure que la plus grande des constituantes...
Invité, affichez le quiz :

Stage : INITELEC






